Guide de validation des progiciels de calcul de structure Guide de validation des progiciels de calcul de structure| sommaire du guide de validation |
|
calcul poutre | calcul coques
|
Les exemples présentés dans ce document sont extraits du "Guide de validation des progiciels de calcul de structures" publié par l'AFNOR.
SSLS01 PLAQUE RECTANGULAIRE EN PORTE-A-FAUX
SSLS02 PLAQUE CARREE SIMPLEMENT SUPPORTEE
SSLS03 PLAQUE CIRCULAIRE SOUS CHARGE UNIFORME
SSLS04 POUTRE A SECTION EN Z
SSLS05 POUTRE CAISSON EN TORSION
SSLS06 CYLINDRE MINCE SOUS PRESSION RADIALE UNIFORME
SSLS07 CYLINDRE SOUS CHARGE AXIALE UNIFORME
SSLS08 CYLINDRE SOUS PRESSION HYDROSTATIQUE
SSLS09 CYLINDRE SOUS SON POIDS PROPRE
SSLS10 TORE SOUS PRESSION INTERNE UNIFORME
SSLS19 COQUE CYLINDRIQUE SOUMISE A SON POIDS PROPRE
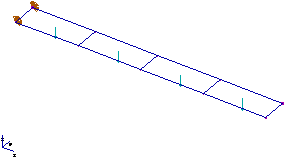Plaque de longueur l=1m, de largeur b=0.1m, d'épaisseur h=0.005m en acier
(E=2.1E11 Pa) encastrée à un extrémité soumise à une pression uniforme p= -1700 Pa.
La théorie des poutres donne la flèche suivante:
w = p b l4/(8 EI), I = b h3/12, w= -0.09714 m
La théorie classique des poutres ne représente pas exactement la déformation des
plaques, car une poutre ne prend pas en compte la variation de flèche dans la section
dans la direction transverse (y), ni l'assouplissement dû au cisaillement transverse.
| nombre de mailles (en x) |
flèche (1 maille en y) (m) |
flèche au centre (2 mailles en y) |
| 1 | -0.0948 | -0.0948 |
| 2 | -0.09317 | -0.0931 |
| 3 | -0.09424 | -0.0941 |
| 4 | -0.09482 | -0.0945 |
| 5 | -0.0952 | -0.0948 |
| 6 | -0.0954 | -0.095 |
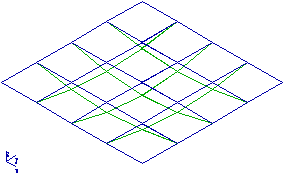Plaque carrée de largeur l=1m, d'épaisseur h=0.01m simplement supportée
sur le contour (Y=0.5
dz=0, dqy=0; Z=0.5, dz=0, dqz=0).
Matériau: E=2.1E11 Pa, nu=0.3 densité=7950 kg.m-3
Champ de gravité (pesanteur) g=9.81 m.s-2.
Les calculs avec des coques "épaisses" (prise en compte de la déformée
associée au cisaillement
transverse) fournissent des flèches plus défavorables que des calculs avec des coques
minces
(hypothèse de Love-Kirchhoff w=0.158mm):
| nombre de mailles par côté |
flèche au centre (mm) avec « coque épaisse » |
| 2 | 0.129 |
| 4 | 0.161=> précision suffisante à partir de 4 divisions |
| 6 | 0.163 |
| 8 | 0.164 |
NB. La différence de la valeur maximale des contraintes calculées aux points de Gauss
est de 5% entre le
maillage grossier 4x4 et le maillage plus fin 8x8.
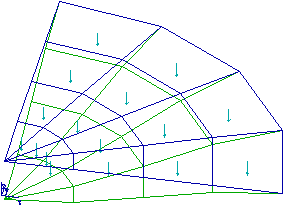Plaque circulaire encastrée au bord de rayon r=1m, d'épaisseur h=0.005m
soumise à une pression
uniforme p=-1000Pa.
Un quart de la plaque seulement est modélisée avec des plans de symétrie. Dans le plan
de symétrie
XoZ, les blocages sont dy=0, dqx = dqz=0; dans le plan YoZ, dx=0, dqy = dqz=0. Attention,
le
noeud central est entièrement bloqué sauf en z (ce noeud cumule les deux conditions de
symétrie).
La plaque est divisée en 4 secteurs. L'augmentation des divisions selon le rayon augmente
la
précision, toutefois 4 sections suffisent pour atteindre une précision sur la flèche de
l'ordre de 0.5%:
| divisions | flèche (mm) |
| 1 | 7.668 |
| 2 | 6.710 |
| 3 | 6.580 |
| 4 | 6.534 |
| 5 | 6.512 |
| 6 | 6.50 |
Poutre Z soumise à un cisaillement à son extrémité.
déplacement du point A: x= -0.000749, y=0.005676, z=-0.007151
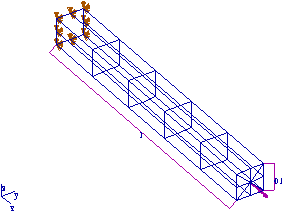Poutre caisson encastrée à son extrémité soumise à un moment M=10 N.m
à l'autre extrémité
(noeuds reliés au point central par des barres rigides).
Déplacement du point B (0.8, -0.05, 0)
z= -9.87E-6 m, qx = 0.197E-4 rad.
Contrainte sxy maximale = 116 000 Pa.
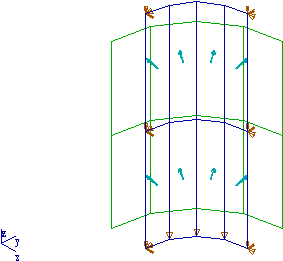Un cylindre de rayon R=1m et de hauteur L=4m, d'épaisseur h=0.02m est
soumis à une pression interne p=10 000Pa.
Un quart de cylindre seulement est modélisé avec 2 plans de symétrie (XoZ) et (Y0Z)..
La solution analytique pour une coque mince conduit à:
contrainte de Mises S= 500E3 Pa.
la dilatation radiale dR = 2.38 E-6m
la variation de hauteur dL = -2.86 E-6m
La précision de la solution dépend du nombre N de secteurs employés dans la
modélisation (avec coque épaisse):
| N secteurs | S (x 103 Pa) | dR (x 10-6 m) | -dL (x 10-6 m) |
| 2 | 462 -7.6% | 2.12 | 2.64 |
| 3 | 483 -3.4% | 2.3 | 2.76 |
| 4 (figure) | 490 -2% | 2.34 | 2.80 |
| 5 | 494 -1.2% | 2.35 | 2.82 |
| 6 | 496 -0.8% | 2.36 | 2.83 |
| 12 | 499 -0.2% | 2.36 | 2.85 |
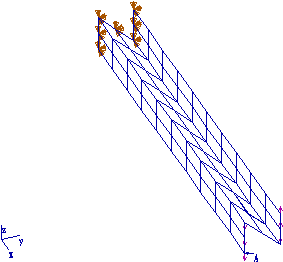
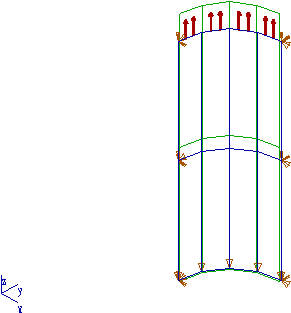Un cylindre de rayon R=1m et de hauteur L=4m, d'épaisseur h=0.02m est
soumis à une traction
uniforme q=10 000 N/m.
La solution analytique pour une coque mince conduit à:
contrainte axiale s= 500E3 Pa.
la dilatation radiale dR = -0.714E-6 m
la variation de hauteur dL = 9.52E-6 m
NB. pour appliquer une charge linéique sur le bord supérieur du cylindre, suivre les
opérations
suivantes:
1. mailler la ligne supérieure du cylindre par des éléments de type "barre
élastique" (ROD).
2. appliquer une charge linéique sur ces barres élastiques.
Une charge répartie P sur une barre élastique de longueur L ne crée pas de moment
fléchissant sur
cette barre. Cette charge est donc équivalente à deux charges concentrées sur chaque
extrémité de
la barre d'intensité P.L/2.
Si la barre élastique est posée sur une coque, on peut choisir une barre de section
nulle AR=0 pour
que cette barre ne rigidifie pas la structure.
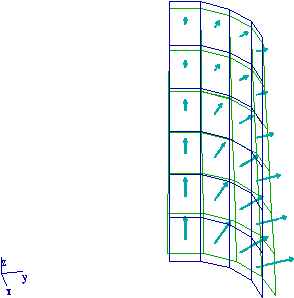Un cylindre de rayon R=1m et de hauteur L=4m, d'épaisseur h=0.02m est
soumis à une pression
hydrostatique 20000Pa*(1-z/L).
La solution analytique pour une coque mince conduit à:
la dilatation radiale dR(z=L/2) = 2.38E-6 m
la variation de hauteur dL(z=L) = -2.86E-6
Pour modéliser finement la variation de pression en fonction de la hauteur, il est
nécessaire de diviser le cylindre sur sa hauteur en éléments (la pression est constante
sur un élément donné).
Avec 6 divisions:
dR(z=L/2) = 2.335E-6 (-1.9%)
dL(z=L) = -2.802E-6 (-2%)
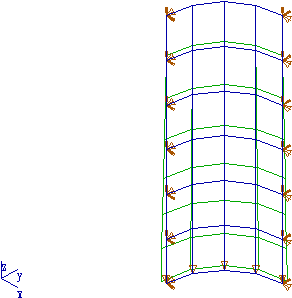Un cylindre de rayon R=1m et de hauteur L=4m, d'épaisseur h=0.02m est
soumis à son poids
propre 7850 kg/m3 * 10 m/s2.
La solution analytique pour une coque mince conduit à:
contrainte axiale s(z=0)= 3.14E5 Pa.
la dilatation radiale dR(z=0) = 4.49E-7 m
la variation de hauteur dL(z=L) = -2.99E-6
La solution obtenue avec le maillage ci-contre est:
s(z=0)= 2.89E5 Pa. (-8%)
dR(z=0) = 4.247E-7 m (-5%)
dL(z=L) = -2.99E-6 (0%)
NB. L'accroissement d'éléments dans le sens vertical Z permet de mieux répartir la
distribution des
efforts du poids propre.
Pour mailler un tore à partir d'arcs de cercles, il faut utiliser des
surfaces de type "surfaces réglées tore-cylindre"; si la surface de maillage
est simplement une "surface réglée", cette surface n'est pas exactement un
tore.
Le tore ci-contre a un demi-diamètre moyen a=2m, un rayon de tube b=1m, une épaisseur
h=0.02m. La pression interne est p=10000Pa.
| contraintes principales | solution analytique | 4 secteurs | 8 secteurs pour un quart de tore |
| S22 (MPa) | 0.25 | 0.22 (-13%) |
0.24 (-4%) |
| S11 (MPa) (r=a-b) | 0.75 | 0.71 (-5%) |
0.743 (-0.9%) |
| S11 (MPa) (r=a+b) | .0417 | 0.402 (-3.5%) |
0.414 (-0.7%) |
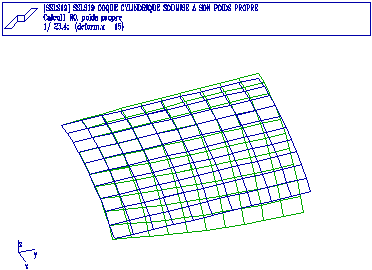Une voute cylindrique de rayon R=3m, de longueur L=6m formant un arc d'angle
2a (a=40 degrés) est soumise à une charge volumique 208 300 N/m3.
Un quart de la voute est modélisé, les résultats ci-dessous indiquent le déplacement
maximal vertical dZ au noeud B [coordonnées x=R sina, y=L/2, z=R cos(a)] et la flèche WB
au point de Gauss le plus proche de B. La solution de référence donnée par le guide
AFNOR est dZ = 3.7 cm (±2%).
Cette structure nécessite une modélisation assez fine car la voute présente une déformée assez relativement complexe avec une double inversion des sens de flexion.