| sommaire du guide de validation |
Les exemples présentés dans ce document sont extraits du "Guide de validation des progiciels de calcul de structures"
publié par l'AFNOR 1990 (ISBN 2-12-486611-7).
Ces tests ont été élaborés par la Société Française des Mécaniciens (SFM) avec
pour objectif de "contribuer à l'amélioration de la qualité et de la fiabilité
des progiciels de calcul de structures, outils indispensables à la conception et au
dimensionnement des équipements mécaniques".
SSLL01 Poutre élancée sur deux appuis encastrés
SSLL02 Poutre courte sur deux appuis articulés
SSLL03 Poutre élancée sur trois appuis
SSLL04 Structure spatiale rotulée sur appuis élastiques
SSLL05 Bilame: poutres encastrées reliées par un élément
indéformable
SSLL06 Arc mince encastré en flexion plane
SSLL07 Arc mince encastré en flexion hors plan
SSLL08 Arc mince bi-articulé en flexion plane
SSLL09 Système de deux barres à trois rotules
SSLL10 Portique à liaisons latérales
SSLL11 Treillis de barres articulées sous une charge ponctuelle
SSLL12 Système triangulé de barres articulées
SSLL13 Poutre sous-tendue
SSLL14 Portique plan articulé en pied
SSLL15 Poutre sur sol élastique, extrémités libres
SSLL16 Poutre sur sol élastique, extrémités articulées
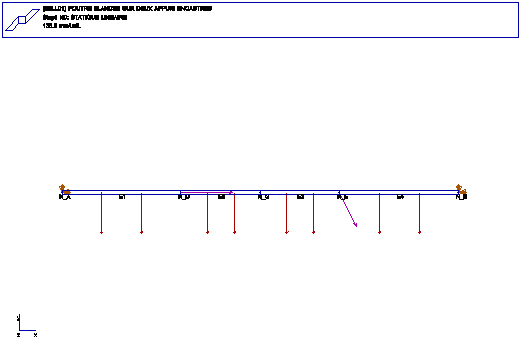
FONCTIONS: POUTRE DROITE ELANCEE, FLEXION DANS LE PLAN,
TRACTION-COMPRESSION
A-----------D----G-----E---------B
L= 1 m
I= 1.7E-8 m4
E= 2.1E11 Pa
noeud A,B: encastres
noeud D: effort axial F1= 30 000 N, couple C= -3000 Nm
noeud E: effort axial F2 = 10 000 N, effort tranchant F= -20 000 N
charge repartie sur toute la longueur AB: -24 000 N/m
abscisses A (0.0), D (0.3), E (0.7), B (1.0)
Solution analytique:
en G (centre de la poutre)
effort tranchant -540 N
moment flechissant 2800 Nm
fleche -4.9E-2 m
en A
reaction horizontale -24 000 N
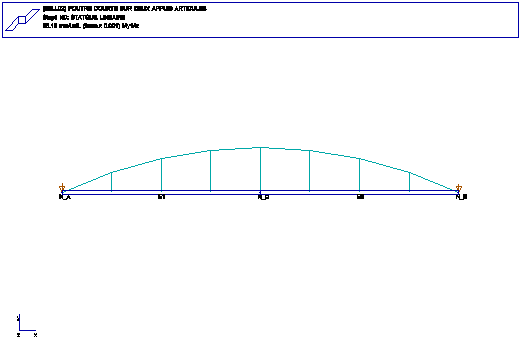
ANALYSE: STATIQUE (PROBLEME PLAN)
TEST: ELEMENTAIRE
FONCTIONS: POUTRE DROITE COURTE, FLEXION DANS LE PLAN, DEFORMATION
D'EFFORT TRANCHANT
A---------------C----------------B
L= 1.44 m longueur AB
A= 31.0E-4 m2 aire
IZZ= 2810.0E-8 m4 inertie
SRY= 2.42 coefficient de
cisaillement
E= 2.0E11 Pa
nu= 0.3
NOEDS A,B: ARTICULES
FORCE UNIFORMEMENT REPARTIE SUR AB -1.0E5 N/m
Solution analytique:
FLECHE= v1 + v2
v1 = -5.P.L**4/(384.E.IZZ)
v2 = -L*L.P*SRY/(8.AR.G) effet du cisaillement transverse
FLECHE EN C -1.25926E-3 (avec effet du cisaillement transverse)
FLECHE EN C -0.9962E-3 (poutre elancee, non prise en compte du
cisaillement transverse)
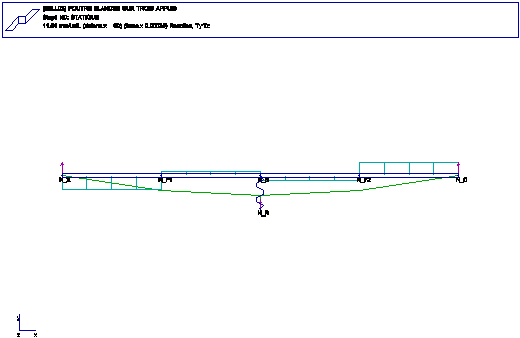
ANALYSE: STATIQUE (PROBLEME PLAN)
TEST: ELEMENTAIRE
FONCTIONS: POUTRE DROITE ELANCEE, FLEXION DANS LE PLAN, LIAISON
ELASTIQUE DISCRETE
F1
F2
A---------------B--------------C
L(AB)=L(BC)=2L= 6 m
IZZ= 6.3E-4 m4
E= 2.1E11 Pa
F= -42E3 N
noeud A,C: libre en rotation RY
noeud B: point d'appui d'un ressort vertical (Ky= 2.1E6 N/m)
la poutre a pour longueur 4L=12m (entre A et C) et
deux forces concentrees (F) sont appliquees aux abscisses L et 3L.
Calcul: FLECHE EN B -0.010 m, REACTION AU SOL 21000 N
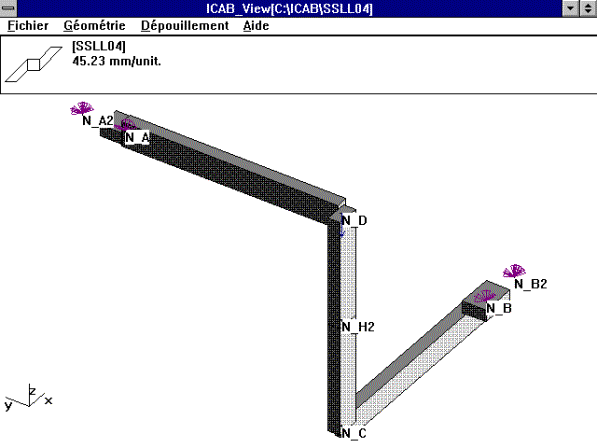
FONCTIONS: POUTRE DROITE ELANCEE, FLEXION, LIAISON ELASTIQUE
DISCRETE
A (Oy) L= 2m
Iyy=Izz= 1E-6 m4
TC= 2E-6 m4
B(Ox) A = 1E-3 m2
E = 2.1E11 Pa
G = 7.875E10 Pa (NU=1/3)
noeud A: Theta(Y)=0, Ky=52500N/m, Ry=Rz=52500 Nm/rad
noeud B: Theta(X)=0, Kx=52500N/m, Ry=Rz=52500 Nm/rad
charge au point D: Fz= -10E3N
La modelisation de la rotule en H est assuree avec l'entite
CONSTRAINT(TYPE=COUPLE)
Moments au point A: Mx=-1562, My=8438, Mz= -3125
Deplacement en A: X=0, Y=-29.76E-3, Z=0, RX=0.16073, RY=0, RZ=-0.059516,
Deplacement en D: X=-0.13887, Y=-29.78E-3, Z=-0.37007
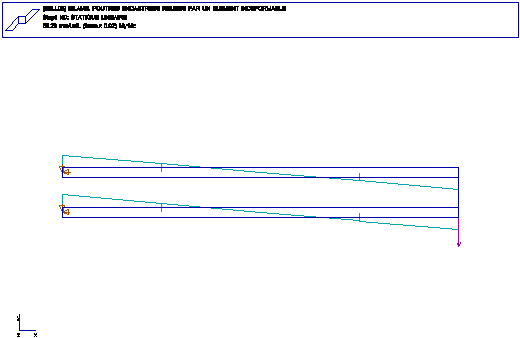
FONCTIONS: POUTRE DROITE ELANCEE, FLEXION DANS LE PLAN, ELEMENT
INDEFORMABLE
A-----------B
l
C-----------D
L
L= 2 m distance entre A et B (C et D)
l= 0.2m distance entre B et D relies par une
barre rigide
I= 1.33333E-8 m4 moment d'inertie
AR= 4E-4 section
E= 2.0E11 Pa
F= -1.0E3 N force appliquee vers le bas en D
noeud A,B: encastres
Solution analytique:
en B et D : FLECHE -0.125
en A et B : reaction Fy=500 N, moment 500 Nm (Fx=0.0)
Remarque: cette solution correspond au cas ou les extremite N_B et N_D sont bloquees en
rotation RZ. Lorsqu'une barre rigide est effectivement utilisee, les noeuds N_B et N_D
subissent des deplacements en X et RZ.
Dans ce cas, la section des poutres intervient dans la solution. Pour obtenir la solution
avec barre rigide, il suffit de definir la macro _RP (enlever le commentaire devant
"#define _RB_ 1")
Solution avec barre rigide:
Reaction en A Fx= -4983.39, Fy= 500, Mz= 501.661
Deplacement en D x=-0.000124585, y=-0.126246, rz=-0.00124585

FONCTIONS: ARC MINCE, FLEXION DANS LE PLAN
A
|
|
|
-------B
R= 3 m rayon de l'arc
section circulaire creuse De=0.02m, Di=0.016m
section AR=1.131E-4 m2
moment d'inertie Ix=4.637E-9
module E=2.0E11
chargement en B: Fx=10N, Fy=5N, Mz=8N.m
noeud A encastre
Solution analytique:
en B x=0.3791, y=0.2417, rz=0.1654
Reaction en A: Fx= -10.0, Fy= -5.0, Mz=-53.0
Modelisation avec 2 poutres droites, deplacement en B:
x=0.343888 (-9.2%) y=0.24368 (0.8%), rz=0.158718 (-4.0%)
Modelisation avec 4 poutres droites, deplacement en B:
x=0.369899 (-2.4%) y= 0.242041 (0.1%), rz=0.163711 (-1.0%)
Modelisation avec 8 poutres droites, deplacement en B:
x=0.37676 (-0.6%) y= 0.241799 (0%), rz=0.164971 (-0.26%)
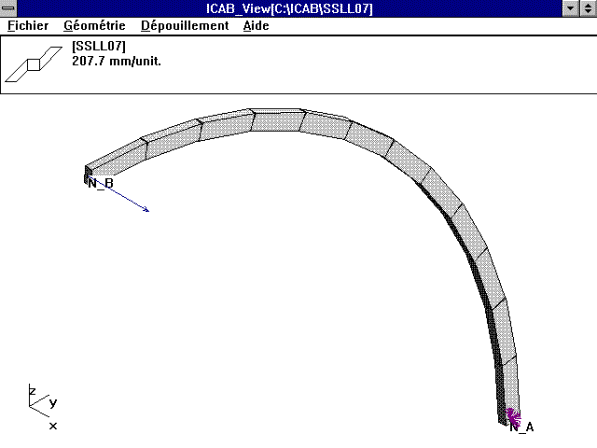
FONCTIONS: ARC MINCE, FLEXION DANS LE PLAN
R= 1 m rayon de l'arc
section circulaire creuse De=0.02m, Di=0.016m
section AR=1.131E-4 m2
moment d'inertie Ix=4.637E-9
module E=2.0E11, NU=0.3
chargement en B: Fx=100N
noeud A encastre
Solution analytique:
en B x=0.13462
angle a 15 deg. Mt= 74.1180, Mf= -96.5925
modelisation avec 7 poutres droites
reaction au noeud A: Fx=-100, My=-100, Mz=-100
deplacement au noeud B: x=0.133051 (-1.1%), ry=0.0552494, rz=0.122664
moments moyens en N_A2 (15 deg.) 73.96, -96.54 N.m

FONCTIONS: ARC MINCE, FLEXION DANS LE PLAN
R= 1 m rayon de l'arc
section circulaire creuse De=0.02m, Di=0.016m
section AR=1.131E-4 m2
moment d'inertie Ix=4.637E-9
module E=2.0E11, NU=0.3
chargement en C: Fy=-100N
noeud A encastre, B bloque dans la direction Y (mais libre en X)
Solution analytique:
en A rz=-3.0774E-2
en B x= 5.3912E-2, rz= 3.0774E-2
en C y=-1.9206E-2
Modelisation avec 2x1 poutres droites (A-C-B seulement)
en A: rz=-3.8123E-2 (23.9%)
en B: x= 5.0828E-2 (-5.7%) rz=3.8123E-2
en C: x= 2.5414E-2 y=-2.5417E-2 (-32.33%)
Modelisation avec 2x2 poutres droites:
en A: rz=-3.2718E-2 (6.3%)
en B: x= 5.2656E-2 (-2.3%) rz=3.2718E-2
en C: x= 2.6328E-2 y=-2.0145E-2 (4.9%)
Modelisation avec 2x4 poutres droites:
en A: rz=-3.1267E-2 (1.6%)
en B: x= 5.3573E-2 (-0.6%) rz= 3.1267E-2
en C: x= 2.6787E-2 y=-1.9395E-2 (0.9%)
Modelisation avec 2x8 poutres droites:
en A: rz=-3.0898E-2 (-0.4%)
en B: x= 5.3826E-2 (-0.16%) rz=3.0898E-2
en C: x= 2.6913E-2 y=-1.9250E-2 (+0.2%)
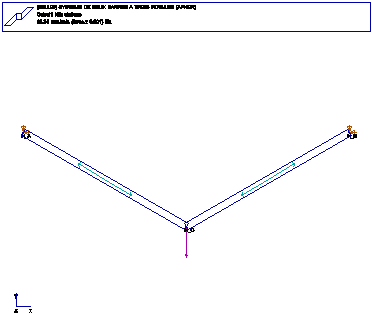
FONCTIONS: TREILLIS PLAN, BARRES ARTICULEES
Calcul:
Deplacement en C: Y= -0.003
contrainte de traction dans les barres 7E+7 Pa soit 21000 N
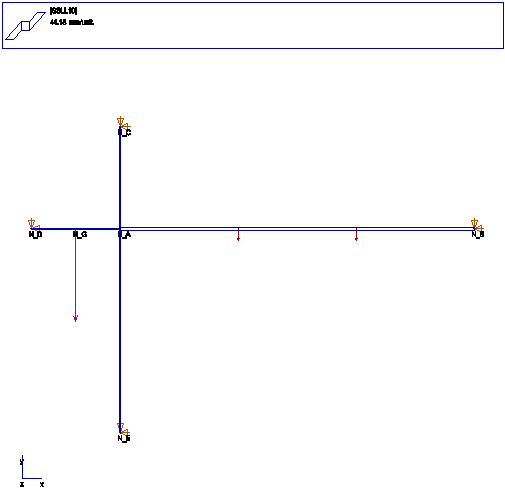
FONCTIONS: FLEXION DANS LE PLAN, PROUTRE DROITE ELANCEE
Calcul:
en A, rotation 0.227118,
Moments M(AB) 11023.72, M(AC) 113.559,
Moments M(AD) -12348.588, M(AE) 1211.2994
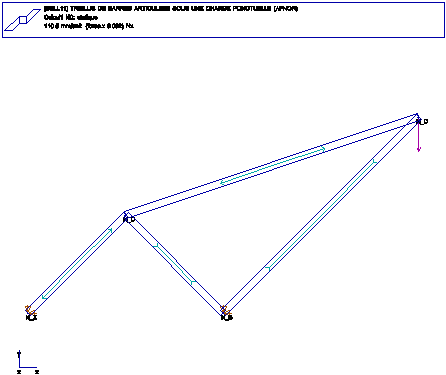
FONCTIONS: TREILLIS PLAN, BARRES ARTICULEES
Calcul:
en C, deplacement 2.6517E-4, 8.839E-5
en D, deplacement 3.47902E-3, -5.60084E-3
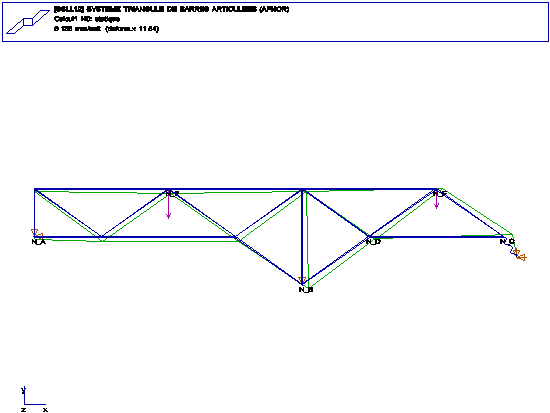
FONCTIONS: POUTRE DROITE ELANCEE, FLEXION DANS LE PLAN,
TRACTION COMPRESSION
Calcul:
effort de traction entre B et D : 43633
deplacement vertical du point D -0.01618
Modelisation: si aucun deplacement n'etait impose en C, une liaison du type MPC pourrait
etre employee pour modeliser le glissement sur plan incline.
CONSTRAINT(TYPE=MPC)
; N_C, Y, 1.0, N_C, X, -2.0;
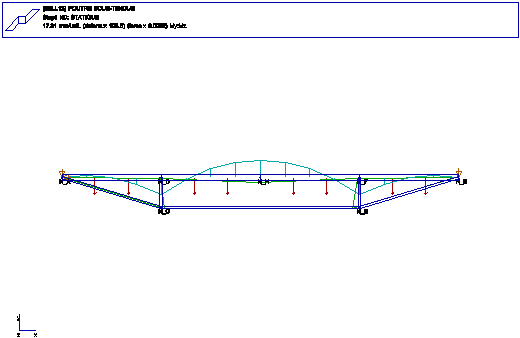
FONCTIONS: BARRES ARTICULEES, POUTRE DROITE, FLEXION DANS LE
PLAN, DEFORMATION D'EFFORT TRANCHANT
Solution analytique:
effort de traction entre C et E : 584584.0
Moment flechissant en H : 49249.5
calcul par progiciels (moyenne selon AFNOR)
deplacement vertical du point D -0.0005428
Modelisation:
La precontrainte dans la barre CE est modelisee en indiquant une tension initiale dans la
barre ou en creant une contraction thermique telle que L.A.(T-T0) = -6.52E-3m
AR=section de la barre,
L=longueur de la barre,
A=coef. dilatation thermique,
T=temperature ambiante,
T0=temperature pour laquelle les dilatations sont nulles
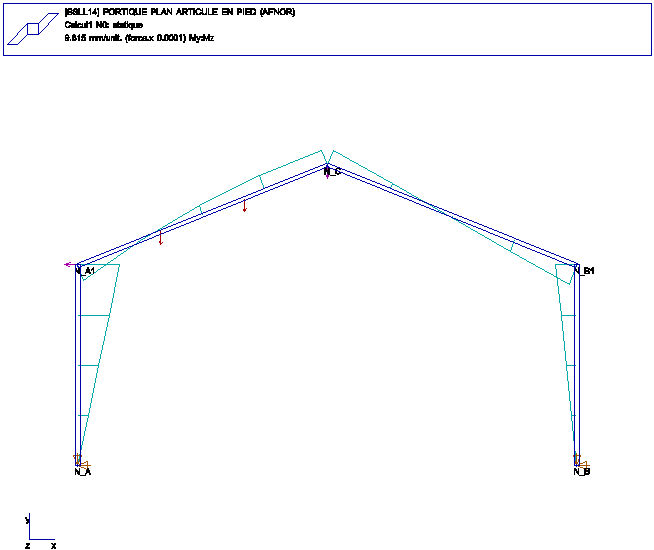
FONCTIONS: POUTRE DROITE ELANCEE, FLEXION DANS LE PLAN,
TRACTION COMPRESSION
hauteur des poteaux 8m, hauteur au sommet du toit (C) 12m
distance entre poteaux 20m.
moments d'inertie pour poteaux 5.0E-4 m4, pout fermes 2.5E-4
force appliquee en C (Y) -100000.0 N, en A1 (X) -10000.0, (RZ) -100000.0
charge repartie verticale entre A1 et C -3000 N/m
Hypothese sur les sections: section carree
noeud A,B: articules
Calcul:
reaction en A (X) 20239.4, (Y) 31500.0
deplacement vertical en C (Y) -0.03072
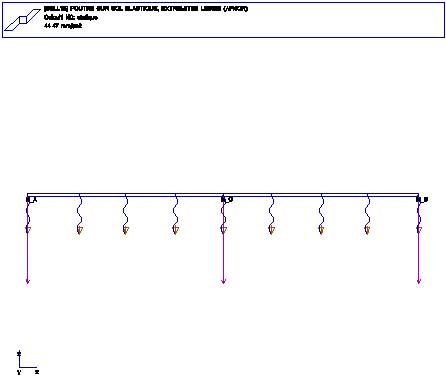
FONCTIONS: POUTRE DROITE ELANCEE, APPUI CONTINU ELASTIQUE, EXTREMITES LIBRES
A-------C-------B
L(AC) = L(CB) = PI*sqrt(10)/2 = 4.967
Force en A, C et B: F= -10E3 N
Raideur lineique= 840E3 N/m
La rigidite du sol elastique est modelise par une succession de ressorts
Solution analytique:
en C, Moment flechissant My=5759 Nm, fleche Z= -0.006844
en A, fleche Z= -0.007854, Rotation RY= -0.000706 rad
calcul avec 2 poutres (avec ecarts par rapport a la solution analytique):
en C, My = 5510 (-4%), Z= -6.92E-3 (+1%)
en A, Z= -7.46E-3 (-5%), RY= -0.326E-3 (-54%)
La modelisation avec 2 poutres seulement est tres satisfaisante, sauf pour le calcul des
rotations aux extremites.
calcul avec 8 poutres:
en C, My = 5901 (+2%), Z= -6.901E-3 (+0.8%)
en A, Z= -7.848E-3 (-0.07%), RY= -0.693E-3 (-2%)
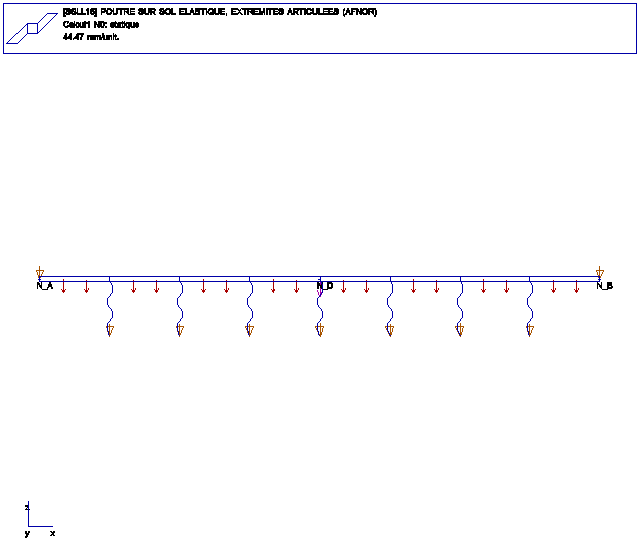
FONCTIONS: POUTRE DROITE ELANCEE, APPUI CONTINU ELASTIQUE, FLEXION DANS LE PLAN
L(AC) = L(CB) = PI*sqrt(10)/2 = 4.967
Force en D: F= -10E3 N
Moments en A: 15E3 Nm, en B -15E3 Nm
charge repartie -5E3 N/m
Raideur lineique= 840E3 N/m
La rigidite du sol elastique est modelise par une succession de ressorts
Solution analytique:
en A, rotation RY= 0.003045, Reaction Fz= 11674
en D, fleche Z= -4.23326E-3, Moment My= 33840
calcul avec 2 poutres (avec ecarts par rapport a la solution analytique):
en A, RZ= 3.076E-3 (+1%), Fz= 13000 (+11%)
en D, Z= -4.232E-3 (-0.03%), Mz= -31870 (-6%)
La modelisation en seulement 2 poutres est satisfaisante
calcul avec 8 poutres:
en A, RZ= 3.045E-3 (0%), Fz= 11760 (+0.7%)
en D, Z= -4.233E-3 (0%), Mz= -33730 (-3%)
"Le guide de validation des progiciels de calcul de structures a pour vocation de servir guide de référence destiné aux concepteurs qui mettent au point des progiciels et qui constituent une une base de données de test largement diffusée, aux étudiants et utilisateurs débutants qui veulent cerner le domaine d'utilisation d'un progiciel particulier, aux utilisateurs chevronnés qui exigent la fiabilité des progiciels proposés et aux organismes de contrôle qui mettent en place des procédures de qualification et de certification reconnues par l'ensemble de la profession.
Un outil à vocation industrielle pour contribuer à l'amélioration de la qualité et de la fiabilité des progiciels de calcul de structures, un outil indispensable à la conception et au dimensionnement des composants mécaniques dans les bureaux d'études.
Les objectifs de la Société Française des Mécaniciens (SFM) ont été de
- rassembler les mécaniciens pour faire le point sur l'utilisation et la validation des progiciels de calcul de structures
- prendre en compte les points de vue du développeur de progiciels et de l'utilisateur
- rédiger un ouvrage de référence qui offre une sélection de tests rigoureusement validés par cinq groupes de travail".