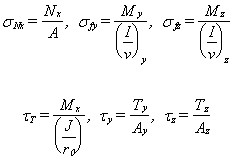
|
Théorie des poutres ICAB Force/CR |
|
documentation ICAB > manuel de référence
Accueil > contraintes dans les poutres
|
Une fois les efforts résultants connus section par section, il est nécessaire de déterminer le champ de contraintes sur chaque section, ou au moins les contraintes maximales sur chaque section.
La contrainte sxx est constante dans la section si la poutre est soumise à un effort de traction ou de compression pur. Dans ce cas, cette contrainte est notée sNx.
La contrainte sxx n'est plus constante si un moment fléchissant simple ou dévié existe. Nous notons sfy la contrainte sxx maximale présente dans la section lorsque la poutre est soumise à un moment fléchissant pur My.
Les cisaillements apparaissent lorsque la poutre est soumise à un moment de torsion ou des efforts tranchants. Un effort tranchant Ty (respectivement Tz) crée une distribution de contrainte de cisaillement txy (respectivement txz). Une torsion, associée à un couple Mx, crée des contraintes txy, txz.
N.B. Ces calculs ne sont rigoureux que lorsque les résultantes des forces et moments sont évalués sur la fibre neutre de la poutre. En effet, une excentration de la fibre neutre provoque en général un couplage de toutes les résultantes; par exemple un effort de traction peut engendrer un effort normal ainsi que des moments fléchissant.
Avec les éléments BEAM_LINEAR proposés par ICAB Force, l'axe (x) correspond à la fibre neutre. Toutefois, la modélisation d'une excentration de la fibre neutre est possible avec l'emploi de barres rigides (RIGID_BAR) placées aux extrémités de la poutre.
Les paramètres de l'entité PROPERTY(TYPE=BEAM_LINEAR) relatifs au calcul de ces contraintes maximales sont AR=A, ARY=Ay, ARZ=Az, IVY=(I/v)y, IVZ=(I/v)z, ITC=(J/r0). Si les sections cisaillées Ay et Az sont nulles, la section totale A est prise en compte pour les calculs des contraintes de cisaillement ty et tz.
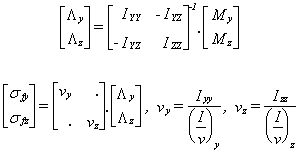
Ces contraintes caractéristiques définissent des majorants pour les contraintes sxx, txy et txz.
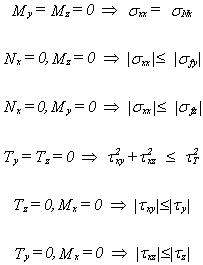
Pour une poutre de section quelconque, la contrainte axiale et le cisaillement sont majorés par:
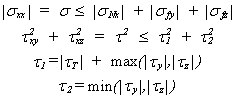
Pour une poutre possédant une symétrie de révolution autour de son axe xx, nous avons:
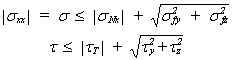
La vérification de sécurité se traduit par:
Sigma/fy < 1
où Sigma est la contrainte maximale de traction ou de compression (règle CM66 1,312). La contrainte Sigma est la somme SNx+Sfy+Sfz. fy est la limite élastique.
La vérification de sécurité se traduit par:
Tau/(0.65 fy) < 1
où Tau est la contrainte maximale de cisaillement (règle CM66 1,313). La contrainte maximale de cisaillement est majorée par t, telle que Tau2 = (Tau1)2+(Tau2)2.
Le critère de Von Mises est utilisé pour déterminer si un matériau isotrope subit une plastification. Pour un tenseur de contrainte symétrique quelconque, le critère de non-plastification est:
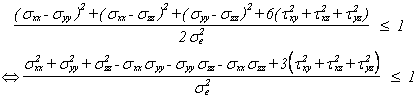
Dans le cas d'une poutre, nous avons:
![]()
Pour un tube sous pression, c’est-à-dire avec une contrainte de membrane stt, le critère de Mises est :
![]()
avec :
NB. Le critère de Mises calculé par ICAB correspond à la racine carrée de l'expression indiquée ci-dessus de manière à rendre ce critère proportionnel à la charge appliquée.
Le critère de Von Mises n'est pas mentionné dans les règles CM66. Toutefois, ce critère est calculé par ICAB dans la mesure où il rend compte d'un état de contrainte quelconque. Pour un cisaillement pur, la plastification apparaît lorsque Tau = S/sqrt(3) = 0.58S, alors que les règles CM66 prévoient une vérification de sécurité par Tau < 0.65S (paragraphe 1,313). L'application du critère de Mises place donc le concepteur en sécurité.
Exemple: fy = 235 MPa pour l'acier S235 (référence EN10025 citée dans l'Eurocode 3).
Le critère de Von Mises ne peut s'appliquer qu'à des matériaux isotropes. Dans le cas de composites ou du bois, les contraintes admissibles dépendent non seulement de la direction de sollicitation mais également du sens de traction ou compression.
Le critère de Tsai-Wu généralise le critère de Von Mises à des matériaux orthotropes dont les contraintes admissibles dans les 3 axes d'orthotropie sont les suivantes:
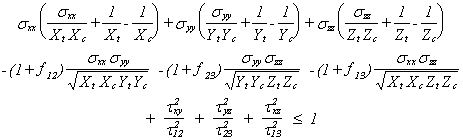
NB. Le critère de TsaiWu calculé par ICAB correspond à la racine carrée de l'expression indiquée ci-dessus.
Pour un matériau isotrope transverse, le critère de Tsai-Wu est identique au critère de Hill si:
Le critère de Tsai-Wu est identique au critère de Von Mises si:
Valeurs par défaut: si toutes les contraintes admissibles ne sont pas indiquées dans les caractéristiques du matériau, alors les valeurs suivantes sont appliquées:
Si certaines valeurs sont encore nulles après les affectations par défaut, alors ces valeurs sont considérées comme infinies, ce qui revient à considérer que ces contraintes admissibles sont très grandes. Par exemple, si Yc=0, alors les calculs sont menés en prenant 1/Yc =0.